Maximizing the Value of a Common ACT Math Strategy

Any student who has ever typed “ACT math tips” into an internet search bar is almost certainly familiar with the strategy of plugging in the answer choices on the ACT Math Section. The upside to this strategy is clear: if students test each answer choice, they must eventually find the correct one. However, this method can often be quite time consuming and can even be ineffective on certain problems. Much like any tool, this strategy will be most useful to students if they are able to understand not only how to use it, but how to do so effectively.
When does the strategy work?
Unfortunately, not all questions on the ACT allow students to test the answer choices. To determine if the strategy is viable for a given question, students can begin by looking at the structure of the answer choices. Firstly, the answer must be in numerical form. While plugging in variables or expressions might be possible in some instances, it is often ineffective or might require the same knowledge that would be necessary to solve the problem outright. Next, students should identify what the numbers in the answer choices represent. If they represent a variable found within the problem, then the strategy should work. However, if the number represents something else (the number of solutions, the difference between two values, etc.), the strategy will not work for that problem. Consider the following examples:
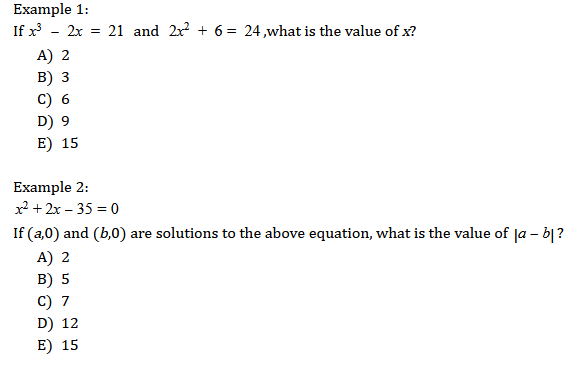
In example 1, the answer choices all represent different values of x. Since the value x is in the question itself, the answer choices can be plugged back into the equation until it produces a mathematically true statement. In this case, the correct answer would be choice B. 3³ - 2(3) = 21 and 2(3)² + 2(3) = 24.
However, in example 2, the answer choices don’t represent any value found within the question. Instead, they measure the absolute value of the difference between the two solutions of the problem. Therefore, there is no place for students to plug in the answer choices correctly. It’s also worth noting that the answer choices are designed to catch students relying on this strategy (or those who don’t read the question carefully). If a student chose to plug in choice B for x in the equation, the equation would be correct, but it would not answer the question.
Where to Begin?
When students recognize that they can plug in the answer choices, should they simply plug in each answer choice randomly until they find the correct answer? They certainly could do so, but in order to maximize the value of this strategy, it is often best to start with the answer choice of middle value. This often provides students with valuable information and can minimize the amount of choices students need to plug in.

Students should note that answer choices typically are ordered by ascending value (Choice A < Choice B < Choice C, etc.). Because of this, the value of answer choice C is almost always between the value of the other options. By testing answer C, students will find that if Sam has rented the bike for 5 hours, he would have paid $10 for the rental plus $3/hour for five hours, resulting in a total of $25, which is greater than the $19 total he paid in the question. Not only does this prove that answer C is incorrect, it also shows that answers D and E must also be incorrect. If Sam were to keep the bike out for longer than 5 hours, his total would continue to increase, but we know his total was actually less than the $25 we found in choice C. Therefore, the answer must be either A or B. Next we can plug in either of the remaining choices: either it will be correct or it will eliminate all but one remaining answer. If the student plugs in choice B, they will find that he spent $10 plus $3/hour for three hours, resulting in a total of $19; thus choice B must be correct.
Ultimately, plugging in the answer choices can be both useful to students as well as frustrating. Few students will ever grow to be confident in their math abilities as they “plug and chug” their way through math sections; it’s time consuming and only partially effective. However, by mastering how and when to use the strategy to its fullest, students can actually use it to support their answers and manage their time on difficult questions.


