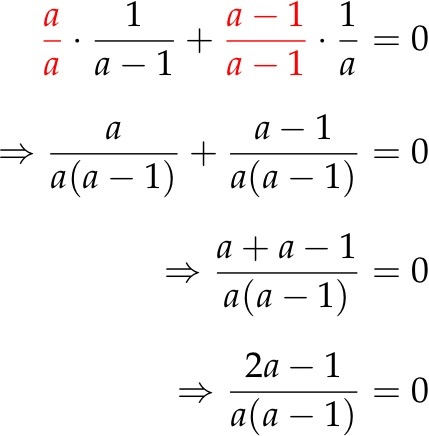
How can understanding one mathematics concept help students drastically increase their SAT math scores? Read more to find out!
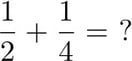
A common error is to assume that we can simply add the top numbers (the numerators) and add the bottom numbers (the denominators) to get our answer. If we did so here, we would get the following.
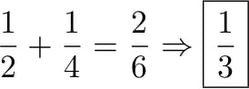
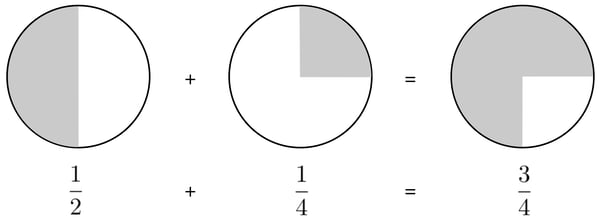
This makes it very obvious why 1/3 is not the correct answer.
Arithmetically, we get the same result by turning the denominator of the first fraction (one-half) into 4, which is the least common denominator shared by the two fractions on the left of the equation (see below). To do so, we multiply the top and bottom of the fraction by 2. By making the denominators the same, we can work with quantities that can be related directly.
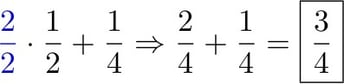
The simplicity of this concept is also the root of an irony: it's one of the many simple things that go by the wayside when students start learning more advanced math. As soon as variables and more sophisticated algebraic expressions are introduced, students become overwhelmed and tend to panic or simply forget how to reason through the problem.
This is a big deal because a huge chunk of the SAT's Math–No Calculator section tests algebraic manipulation with fractions. In fact, on a recent SAT, this concept was tested no fewer than three times in the 20-question No Calculator section. (That's 15% of the questions in the section!) Thus, students who lack fluidity with finding least common denominators are at a significant disadvantage when they encounter this section, which eschews the calculator-as-crutch.
Here's an example of what a student could be expected to do. Note that this is a "student produced response" question, which requires students to provide a numeric answer rather than to select from a list of multiple choice options.
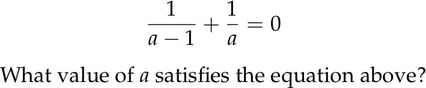
Interestingly, the College Board classifies this as a "hard" problem (the highest level of difficulty it designates), but only because its test creators know that most students have a poor grasp of the fundamental concept explained above. In truth, this should be a piece of cake for most students, because it involves little more than finding a common denominator. What's that? Well, just like 2 and 4 were numbers in the first problem, a – 1 and a represent numbers in this one. We give each fraction what it lacks to get a common denominator, and then add the fractions together, combining the numerators and keeping the denominators the same, just as in the first problem.
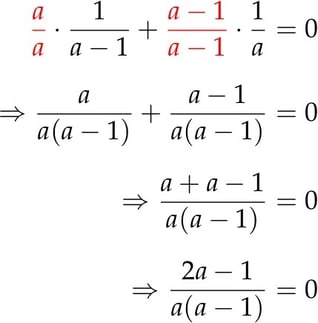
Now, we have a single combined fraction equal to zero. If the fraction gives us zero, that means its numerator must equal zero, because zero divided by anything is what gets us zero. (This assumes the denominator itself can't equal zero, as 0/0 would be undefined, or as I like to call it, the black hole of mathematics.)
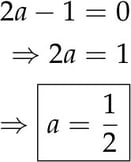
To those of you who haven't taken a math class in 30 years, the steps above may look ugly. However, to students who are actively studying math, this is actually pretty routine.
Here's an example of what a multiple choice question testing the same concept might look like.
Here, we could use a number for a and simply plug in and test, but that's time consuming, and remember, we don't have a calculator: eventually, we're going to have to do arithmetic with fractions anyway, so the algebraic approach is the one to take. We have the same scenario as before––we must find a common denominator to combine the terms. Here, that's just 6a2, because it's easy to multiply the left-side fraction to get there.
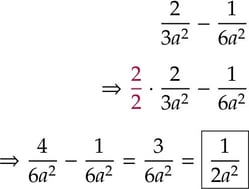
So choice D is correct. Once again, the College Board would rank this as a "hard" question, despite the fact that any student who has successfully completed 6th grade math has at least seen the approaches necessary for solving this problem.
Unfortunately, most students find fractions disproportionately intimidating. (I once had a student tell me matter-of-factly, "I don't do fractions.") There's nothing to be afraid of, though. For those students who feel uncomfortable with fractions, here's my suggestion: brush up. By mastering this one concept, you can increase your SAT math scores by 40-50 points.
