Imagine this: you are standing in line at the concession stand at the movies, and you only have $20 to spend on snacks. You look at the menu and see that a medium popcorn costs $7.10, a soft drink costs $5.25, and a pack of candy costs $4.95, and you need to figure out whether your $20 will cover all three items plus an eight percent sales tax. Would you:
a) Frantically pull up the calculator on your phone, add the prices of the three items together, then multiply by 1.08 to determine the total including sales tax.b) Find some scrap paper and do the same calculations manually.
c) Figure the popcorn is about $7, the drink is about $5, the candy is about $5, and the tax should probably be about a dollar or two, and add those numbers together to find the approximate total.
All three methods will yield the same result (yes, you can afford to snack away), but it’s likely that in a real life scenario, you almost certainly would have defaulted to option C. Why? It’s because you intuitively understand that finding the exact price isn’t entirely relevant to your problem. It doesn’t matter whether the total is $19.00 or $18.68 -- you just want to know if it will be less than $20, so coming up with a rounded answer is quicker and more efficient for your purpose. The same logic can be applied to many SAT questions, especially those on the test’s No-Calculator section: since most questions are multiple choice, students don’t necessarily have to find the exact answer; solving for something close to the correct answer is often good enough to answer the question without spending extra time on unimportant details.
Example 1:
Joaquin wants to order a felt table pad to cover the surface of a circular table. He measures the distance around the outer edge of the table and determines the table’s circumference is 10π feet. If the felt costs $2.00 per square foot, approximately how much will Joaquin need to spend to completely cover the surface of the table with the felt pad?
- $60
- $160
- $314
- $600
This question includes a couple of indicators that students likely shouldn’t be concerned about calculating an exact answer. Firstly, the question asks students “approximately, how much money will Joaquin need to spend?”; since the answer will be approximate, any calculations can likely also be approximated. Additionally, the four answer choices are fairly disparate, meaning that it’s unlikely that students would come up with an approximate answer that is close to more than one of these options. Regardless of strategy, students first must identify what information is known (the price of felt per square foot and the circumference of the table), what they need to find out (the cost to cover the table with felt), and how to use the known information to solve for what they are trying to find (use the known circumference to solve for the area of the table top and multiply by the cost of the felt per square foot). Whether students choose to round or use the exact numbers, the steps will be the same; the difference is in the ease of the calculations within those steps.
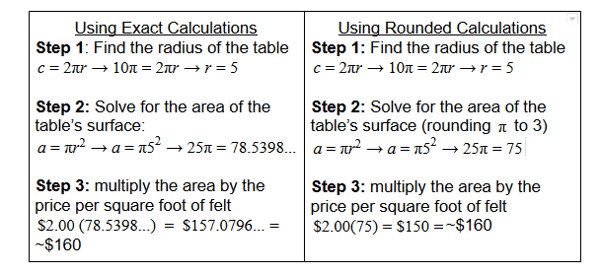
Ultimately, the question required students to round their answer regardless of which method they used, but calculating 3(25) and 2(75) by hand is much quicker and easier than calculating 3.14(25) and 2(78.5398) by hand.
As we can see in the next example, this strategy can also apply to more straightforward algebra problems where rounding might not seem as obvious an approach.
Example 2:
Students could solve algebraically by using the table to solve for the slope and y-intercept, then matching those terms with the appropriate slope-intercept form in the answer choices, or students could simply plug in a known pair of values for x and f(x) into each answer choice. No matter which method a student chooses, rounding these numbers will almost certainly be quicker and more efficient than trying to solve the problem with the exact numbers given. For example, let’s see what the calculations might look like if a student decided to plug values into the answer choices:
I decided to time myself doing the exact calculations by hand for this problem versus solving with rounded numbers to see just how much of a difference this strategy makes. Solving manually with the exact numbers, I took an average of 14 seconds per answer choice, meaning it would take up to 56 seconds for me to try all of the answer choices. If we account for time spent reading the question, determining how to solve, etc., using such a method for this problem would likely take somewhere between a minute and a minute and a half to solve. By comparison, it only took about three seconds per answer choice when rounding, roughly 12 seconds to test all four answers. Again, accounting for other aspects of the problem, the question would probably take 30-60 seconds to solve: nearly half the time it would have taken to solve with the exact numbers!
An important thing to remember when dealing with the SAT’s No-Calculator Math section is that it is not designed to simply test students on their ability to perform calculations but rather to test them on their understanding of mathematical principles or concepts. In fact, if students find themselves dealing with numbers that leave them wishing they could pull out their calculators, it’s usually a good sign that there might be an easier way to find the correct answer. Oftentimes, this means taking a more outside-the-box approach than what students might try on a math test in school.
