Swing at the Slow Pitches

As an SAT® and ACT® tutor, I hear a wide range of concerns from students hoping to significantly improve their test scores. Among the most common of these is that they feel lost when they reach the tests’ trickiest questions, a fear of which can squelch students’ confidence at the most inopportune times.
Students are often relieved, then, when I give them license to do what might seem unthinkable: just ignore those questions…at least at first. Unless your test scores are already very high, achieving significant improvements on the SAT or ACT usually doesn’t require tackling the most difficult problems. Those are the sorts of questions that separate 1500s from 1600s on the SAT or 35s from 36s on the ACT.
If you’re scoring between the 25th and 75th percentiles on these tests—in other words, if you’re among the middle-50% of scorers—take some crucial advice: swing at the slow pitches. Rather than attempting to grasp every concept that’s tested, focus instead on simply being as accurate as you can be on the tests’ simpler, more straightforward problems.
To see why this works, let’s look first at a “fast pitch” question that you might see on the Math section of an SAT exam.
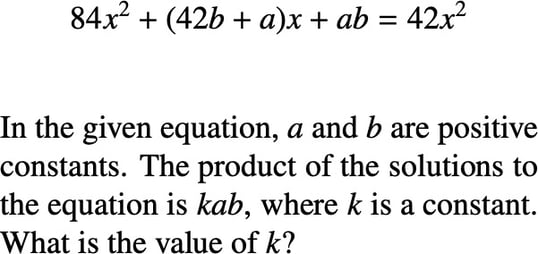
What makes a question like this so tough is that each of the routes we could take to solve it has a high barrier to entry. The best way to solve the problem—which, not incidentally, is also the fastest—is to subtract 42x2 from both sides of the equation in order to set the quadratic polynomial equal to zero, after which we can deploy a special formula to determine the product of its solutions.
42x2 + (42b + a)x + ab = 0
The formula tells us that the product of the solutions to a quadratic equation written in the form ax2 + bx + c = 0 is equivalent to c / a. Here, a = 42 and c =ab, so the product of the solutions of this equation is (ab) / 42. And since it’s given by the problem that the product of the solutions is equal to kab, we can express this fact as:
![]()
Dividing both sides by ab then yields
![]()
as our solution.
That process isn’t terribly complicated…provided that you know it. Unfortunately, most students who take the SAT and ACT aren’t aware of this easy fix. In order to solve the problem without it, a student would need to perform excessive algebraic manipulations, creating a gigantic time suck.
Allow me to illustrate just how tedious and protracted such a process could be.
To start, you’ll notice that the equation has a squared term in it. This tells us that we’re looking at a quadratic equation. The standard form of a quadratic equation is written ax2 + bx + c = 0, so we should start by simplifying the expression such that everything is set equal to zero. As before,
42x2 + (42b + a)x + ab = 0.
From here, we’ll want to distribute the x into the parentheses, giving us
42x2 + 42bx + ax + ab = 0.
I’m confident that most students of intermediate math proficiency could get about this far. But for many, the path forward from here can seem elusive—and it’s not hard to understand why. The question asks for the value of k, and there’s no k in the equation as currently expressed. And in order to find k, the question suggests that we need to find the product of the equation’s solutions, a task complicated by the fact that we have three unknown constants to reckon with.
To make any further progress, a student would require an additional skill that can’t be memorized or solved by brute force: the skill of pattern recognition. A sharp eye will notice that among the four terms in the equation above, we can create two pairs of terms, each of which share a common factor.
(42x2 + 42bx) + (ax + ab) = 0.
We can then factor out the greatest common factor of each group of terms.
42x(x + b) + a(x + b) = 0.
The two factors, 42x and a, can now be grouped into their own set of parentheses, and the two occurrences of (x + b) can be consolidated into a single set of parentheses...
(42x + a)(x + b) = 0
...after which both binomials can be individually set to zero and subsequently solved for x.
42x + a = 0 ---> x = –a /42
x + b = 0 ---> x = –b
When we multiply these solutions together, we get ab / 42. Since the question stipulates that k is the coefficient of ab, where kab is the product of the equation’s solutions, the value of k is 1/42.
Having fun yet? Me neither. This is the sort of question that is not only unhelpful for “middle-percentile scorers” to spend time on, but is also actively detrimental for them to focus on.
Rather than spend three full minutes working through a problem like the one above, most students would be better off using that time to knock out three one-minute questions instead. Even if the “fast pitch” question is worth more points than any of the three easier questions individually, a student would still earn more points overall by swinging at—and hitting—all three “slow pitches.” Chances are that they could do so in about the same amount of time, too.
But how can a student distinguish a slow pitch from a fast one? After all, what might seem like a fast pitch to one student may seem to glide leisurely over home plate to another. In other words, no SAT or ACT problem is inherently “difficult,” provided that a student can readily identify how to handle it. How, then, can students decide which pitches they ought to swing at?
Because any one answer to this question is so subjective, adopt the following principle: the speed of a problem’s pitch is the time it takes you to get started on it.
Consider a question that most students would consider a “slow pitch,” such as the one below.
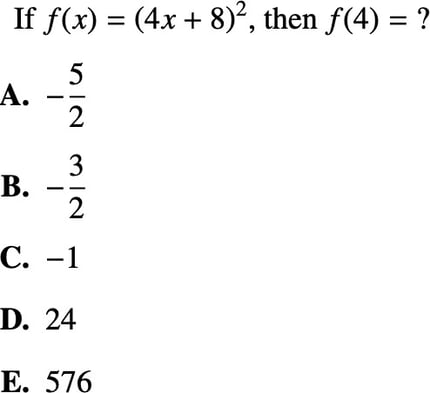
To get started on this problem, all that’s required is an understanding of function notation, a concept far more straightforward than what we saw above. Once a student grasps that when we plug in whatever is in the parentheses of f (x) as our x-value and that the resulting output gives us our y-value, the problem becomes a matter of simply punching numbers into a calculator. As a result, this sort of “slow pitch” problem is far easier to master than the algebraic gymnastics of the problem we considered earlier—an advantage compounded by the fact that slow pitches simply appear more frequently on the SAT and ACT than fast ones do, thus accounting for more total points.
Equally critical but often overlooked are the roles that confidence and momentum play in these scenarios. With sufficient preparation, a student would expend minimal effort on test day answering a “slow pitch” question like the function problem above. The psychological boost they would gain from doing so, however, would be anything but minimal. By learning to quickly and accurately knock many such “slow pitches” out of the park, students will become both more efficient and more confident.
Now, of course, I'm not suggesting that you ignore “fast pitch” problems altogether. What I am suggesting is that there is literally no instance in which a student should focus on learning how to solve very difficult SAT/ACT problems—the ones that have high barriers to entry—before first learning how to tackle simpler ones—the ones that are easier to get started on. By first swinging at the slow pitches that the SAT and ACT throw you, you’ll not only optimally moderate your time for test taking success, but you’ll generate a tailwind of optimism that can eventually be used to help send the faster pitches soaring as well.


